ガウス過程回帰とは？非線形予測と不確実性を解説【機械学習】

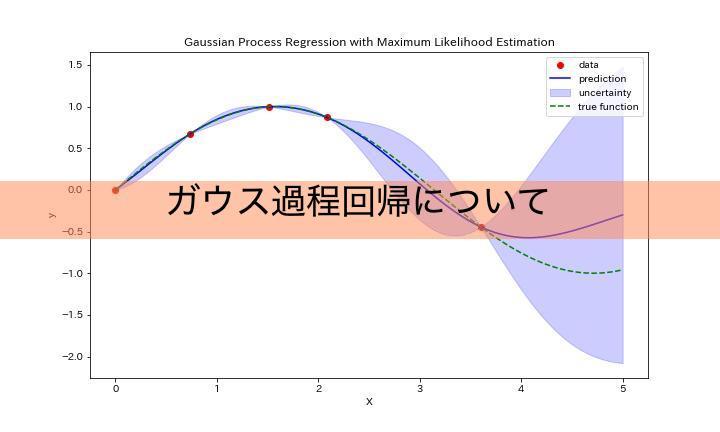
ガウス過程回帰は、機械学習の中でも特に非線形予測と不確実性の定量化に優れた手法です。この手法は、データ間の関係を確率的にモデル化し、予測を行う際に信頼区間を同時に提供します。ガウス過程回帰は、平均関数と共分散関数によって特徴付けられ、これらがモデルの柔軟性と予測精度を決定します。

本記事では、ガウス過程回帰の基本的な概念から、その数学的基盤、そして実際の応用例までを解説します。特に、非線形データに対する予測能力と、予測結果の不確実性をどのように評価するかについて詳しく説明します。また、ガウス過程回帰の利点と課題についても触れ、どのような場面でこの手法が有効かを考察します。

最後に、ガウス過程回帰が時系列分析や機械学習の他の分野でどのように活用されているか、具体的な事例を交えて紹介します。これにより、読者はガウス過程回帰の実践的な価値を理解し、自身のプロジェクトに応用するための基礎を築くことができるでしょう。

イントロダクション

ガウス過程回帰は、機械学習の中でも特に非線形予測と不確実性の定量化に優れた手法です。この手法は、データの背後にある複雑な関係を捉えるために、確率的なアプローチを採用しています。ガウス過程回帰の特徴は、予測値だけでなく、その予測の信頼区間も同時に提供することです。これにより、モデルの出力がどの程度信頼できるかを評価することが可能になります。

ガウス過程回帰は、平均関数と共分散関数によって定義されます。平均関数は予測の中心的な傾向を示し、共分散関数はデータポイント間の関係をモデル化します。特に、共分散関数は、データの非線形性や局所的な変動を捉えるために重要な役割を果たします。この柔軟性により、ガウス過程回帰は、時系列分析や空間データ解析など、さまざまな分野で応用されています。

しかし、ガウス過程回帰にはいくつかの課題もあります。特に、計算コストが高く、大規模なデータセットに対しては適用が難しい点が挙げられます。また、ハイパーパラメータの調整も重要な課題であり、適切な設定がモデルの性能に大きく影響します。これらの課題を克服するため、近年では効率的な近似手法や最適化手法が研究されています。

ガウス過程回帰の基本概念

ガウス過程回帰は、機械学習における非線形回帰問題を扱うための強力な手法です。この手法は、ガウス過程と呼ばれる確率過程を基にしており、入力データと出力データの間の複雑な関係をモデル化します。ガウス過程回帰の特徴は、予測値だけでなく、その不確実性も同時に推定できる点にあります。これにより、予測結果の信頼性を評価することが可能です。

ガウス過程回帰では、平均関数と共分散関数が重要な役割を果たします。平均関数は、入力データに対する出力の期待値を表し、共分散関数は、異なる入力データ間の関係性をモデル化します。特に、共分散関数はカーネル関数とも呼ばれ、データの類似性を定義するために使用されます。このカーネル関数の選択によって、モデルの柔軟性や予測精度が大きく変わります。

ガウス過程回帰のもう一つの利点は、ベイズ的なアプローチを採用していることです。これにより、事前分布と観測データを組み合わせて事後分布を計算し、予測の不確実性を自然に表現できます。この特性は、特に時系列分析やロボティクス、気象予測などの分野で有用です。ただし、計算コストが高いことや、ハイパーパラメータの調整が難しいといった課題もあります。

非線形予測と不確実性の扱い

ガウス過程回帰は、機械学習の中でも特に非線形予測と不確実性の扱いに優れた手法です。従来の線形回帰モデルでは捉えきれない複雑なデータの関係性を、柔軟にモデル化することができます。ガウス過程は、データの背後にある関数を確率的に表現し、平均関数と共分散関数によってその振る舞いを特徴付けます。これにより、予測値だけでなく、その予測の信頼区間も同時に計算できる点が大きな強みです。

ガウス過程回帰のもう一つの特徴は、ベイズ的なアプローチを採用していることです。これにより、モデルの不確実性を自然に表現し、予測の信頼性を評価することが可能になります。特に、データが少ない場合やノイズが多い場合でも、過学習を防ぎつつ、適切な予測を行うことができます。この特性は、時系列分析やロボティクス、実験計画法など、さまざまな分野で活用されています。

ただし、ガウス過程回帰は計算コストが高いという課題もあります。特に、データ数が増えると、共分散行列の計算や逆行列の計算が重くなり、実用上の制約となることがあります。また、ハイパーパラメータの調整も重要なポイントで、適切な設定がモデルの性能を大きく左右します。これらの課題を解決するために、近似手法や効率的なアルゴリズムの研究が進められています。

ガウス過程回帰の特徴と利点

ガウス過程回帰は、非線形関係をモデル化するための強力な手法です。従来の線形回帰とは異なり、データの複雑なパターンを捉えることができます。この手法の最大の特徴は、予測値だけでなく、その不確実性も同時に推定できる点です。これにより、予測結果の信頼性を評価することが可能となります。

ガウス過程回帰の利点の一つは、その柔軟性です。データに応じてモデルが自動的に適応するため、事前に特定の関数形を仮定する必要がありません。また、共分散関数を適切に設計することで、さまざまな種類のデータ構造に対応できます。これにより、時系列データや空間データなど、多様な応用分野で活用されています。

さらに、ガウス過程回帰はベイズ的なアプローチを採用しているため、モデルの不確実性を自然に扱うことができます。これは、特にデータが少ない場合やノイズが多い場合に有用です。ただし、計算コストが高いことや、ハイパーパラメータの調整が難しいといった課題もあります。これらの点を理解し、適切に活用することが重要です。

ガウス過程回帰の応用分野

ガウス過程回帰は、その柔軟性と不確実性の定量化能力から、さまざまな分野で応用されています。特に、時系列分析や予測モデリングにおいて、その強みを発揮します。例えば、金融市場の変動予測や気象データの解析など、非線形な関係性が複雑に絡み合う領域で高い精度を誇ります。また、ロボティクスや自動運転技術においても、センサーデータの処理や環境認識にガウス過程回帰が活用されています。

さらに、医療分野では、患者の病状進行予測や薬剤効果の推定に応用されています。不確実性を考慮した予測が可能であるため、リスク管理や意思決定支援に役立ちます。また、材料科学や化学工学では、実験データの少ない状況下での材料特性の予測やプロセス最適化に利用されています。このように、ガウス過程回帰は、データ駆動型のアプローチが求められる多様な分野で重要な役割を果たしています。

一方で、計算コストの高さやハイパーパラメータの調整の難しさといった課題も存在します。しかし、近年の計算リソースの進化やアルゴリズムの改良により、これらの課題も徐々に克服されつつあります。今後も、ガウス過程回帰は、機械学習の重要な手法として、さらなる発展が期待されています。

ガウス過程回帰の課題と制約

ガウス過程回帰は、その柔軟性と非線形予測能力から多くの分野で活用されていますが、いくつかの課題と制約も存在します。まず、計算コストが高いことが挙げられます。特に、データセットのサイズが大きくなると、共分散行列の計算や逆行列の計算に要する時間が急激に増加します。このため、大規模なデータセットに対しては実用的でない場合があります。

また、ハイパーパラメータの調整が難しいという点も課題です。ガウス過程回帰では、共分散関数のパラメータを適切に設定する必要がありますが、これがモデルの性能に大きく影響します。しかし、これらのパラメータを最適化するためには、多くの場合、計算コストの高い最適化手法を利用する必要があります。

さらに、ガウス過程回帰は、予測の不確実性を定量化できるという利点がありますが、その不確実性が大きすぎると、実用的な予測が難しくなる場合があります。特に、データが少ない領域では、予測の信頼区間が広がり、信頼性の低い結果が得られることがあります。これらの課題を克服するため、さまざまな近似手法やスケーラビリティ向上のための手法が研究されています。

まとめ

ガウス過程回帰は、機械学習における重要な手法の一つであり、特に非線形予測や不確実性の評価に優れています。この手法は、データの背後にある複雑な関係を捉えるために、確率的なアプローチを採用しています。ガウス過程回帰では、平均関数と共分散関数を用いて、入力データに対する出力の分布をモデル化します。これにより、予測値だけでなく、その予測の信頼区間も同時に得ることができます。

ガウス過程回帰の大きな特徴は、その柔軟性にあります。線形モデルでは表現が難しい複雑な非線形関係も、ガウス過程回帰では自然に扱うことが可能です。また、ベイズ的な枠組みを採用しているため、予測の不確実性を定量的に評価できる点も強みです。これにより、時系列分析やロボティクス、さらには強化学習など、さまざまな分野で応用されています。

ただし、ガウス過程回帰にはいくつかの課題もあります。特に、計算コストが高く、大規模なデータセットに対しては適用が難しい場合があります。また、ハイパーパラメータの調整が複雑で、適切な設定を見つけるために多くの試行錯誤が必要となることもあります。それでも、その理論的な美しさと実用性から、ガウス過程回帰は機械学習の分野で重要な位置を占め続けています。

よくある質問

ガウス過程回帰とは何ですか？

ガウス過程回帰（Gaussian Process Regression, GPR）は、非線形データを扱うための強力な機械学習手法の一つです。この手法は、確率的なアプローチを採用しており、入力データと出力データの間の関係をモデル化します。ガウス過程回帰の特徴は、予測値だけでなく、その不確実性も同時に推定できる点にあります。これは、ベイズ的な枠組みに基づいており、データの分布をガウス分布（正規分布）として仮定することで、柔軟なモデリングが可能となります。特に、少量のデータでも高い予測精度を発揮することが知られています。

ガウス過程回帰の利点は何ですか？

ガウス過程回帰の主な利点は、非線形関係を自然に扱えることと、不確実性の定量化が可能な点です。従来の線形回帰モデルでは、複雑な非線形パターンを捉えることが難しい場合がありますが、ガウス過程回帰はカーネル関数を用いることで、データの複雑な構造を柔軟にモデル化できます。また、予測の信頼区間を提供するため、予測結果の信頼性を評価する際に非常に有用です。さらに、ハイパーパラメータの調整が比較的容易であり、データに応じた最適なモデルを構築しやすいことも利点の一つです。

ガウス過程回帰の欠点は何ですか？

ガウス過程回帰の主な欠点は、計算コストが高いことです。特に、データ数が増えると、カーネル行列の逆行列計算が必要となるため、計算量が急激に増加します。このため、大規模なデータセットに対しては適用が難しい場合があります。また、ハイパーパラメータの選択がモデルの性能に大きく影響するため、適切なチューニングが必要です。さらに、解釈が難しいという側面もあり、特に複雑なカーネル関数を使用した場合、モデルの挙動を直感的に理解することが難しくなります。

ガウス過程回帰はどのような分野で活用されていますか？

ガウス過程回帰は、機械学習や統計学の分野で広く活用されています。特に、ロボティクスや制御工学では、システムの動的モデリングやセンサーデータの予測に使用されます。また、気象予測や金融市場の分析など、不確実性が重要な要素となる分野でも応用されています。さらに、医療分野では、患者データに基づく個別化された治療計画の策定や、材料科学では、実験データに基づく新材料の特性予測にも利用されています。このように、ガウス過程回帰は、多様な分野でその有用性が認められています。