Pythonで非線形関数モデリング：多項式回帰とニューラルネットワークの活用

非線形関数モデリングは、データ間の複雑な関係を捉えるための重要な手法です。この記事では、Pythonを使用して非線形関数モデリングを行う方法について解説します。特に、多項式回帰とニューラルネットワークという2つの主要な手法に焦点を当て、それぞれの特徴や適用例を紹介します。これらの手法は、データの特性や目的に応じて使い分けることが重要です。

多項式回帰は、データを多項式関数で近似する手法であり、比較的シンプルで計算コストが低いという利点があります。一方、ニューラルネットワークは、より複雑な非線形関係をモデル化するのに適しており、高い精度を実現できますが、計算コストが高く、モデルの解釈が難しいという課題もあります。

この記事では、scikit-learnやTensorFlow、PyTorchといったPythonライブラリを使用して、これらの手法を実際に実装する方法を説明します。また、非線形関数モデリングのメリットやデメリット、今後の展望についても触れます。データ分析や機械学習に興味のある方にとって、役立つ情報を提供することを目指しています。

イントロダクション

非線形関数モデリングは、データ間の複雑な関係を捉えるための重要な手法です。線形モデルでは表現しきれない複雑なパターンを、非線形関数を用いてモデル化することで、より高精度な予測や分析が可能になります。この記事では、Pythonを用いて非線形関数モデリングを行う方法について、特に多項式回帰とニューラルネットワークに焦点を当てて解説します。

多項式回帰は、非線形関係を捉えるためのシンプルかつ強力な手法です。データに対して多項式をフィットさせることで、線形モデルでは表現できない曲線的な関係をモデル化できます。一方、ニューラルネットワークは、より複雑な非線形関係を捉えるための高度な手法です。多層構造を持つニューラルネットワークは、データの特徴を自動的に学習し、非常に柔軟なモデルを構築することができます。

Pythonには、これらの手法を実装するための豊富なライブラリが存在します。例えば、scikit-learnは多項式回帰を簡単に実装できるツールを提供し、TensorFlowやPyTorchはニューラルネットワークの構築とトレーニングを支援します。これらのツールを活用することで、非線形関数モデリングを効率的に行うことが可能です。

非線形関数モデリングは、高精度な予測を実現する一方で、計算コストが高くなりやすく、モデルの解釈が難しいという課題もあります。しかし、データ分析や機械学習の分野において、その重要性はますます高まっています。本記事を通じて、非線形関数モデリングの基礎と実践的な活用方法を理解し、今後のプロジェクトに役立てていただければ幸いです。

非線形関数モデリングとは

非線形関数モデリングとは、データ間の関係が直線的でない場合に、その複雑な関係を捉えるための手法です。線形モデルでは表現できないような曲線的な関係や、より高度なパターンをモデル化するために用いられます。例えば、自然界や社会現象における多くのデータは、単純な線形関係では説明できないことが多く、非線形関数モデリングが有効です。

この手法の特徴は、柔軟性と高精度な予測にあります。非線形関数モデリングを使用することで、データの背後にある真の関係をより正確に表現し、予測精度を向上させることができます。一方で、モデルの複雑さが増すため、計算コストが高くなり、過学習のリスクも伴います。そのため、適切なモデル選択やハイパーパラメータの調整が重要です。

非線形関数モデリングの代表的な手法として、多項式回帰とニューラルネットワークが挙げられます。多項式回帰は、データを多項式関数で近似するシンプルな手法であり、比較的低コストで実装できます。一方、ニューラルネットワークは、複雑な非線形関係を表現するための強力なツールであり、特に深層学習の分野で広く活用されています。これらの手法を適切に使い分けることで、さまざまなデータセットに対して効果的なモデリングが可能となります。

多項式回帰の基礎

多項式回帰は、非線形関係をモデル化するためのシンプルでありながら強力な手法です。この手法では、入力変数を多項式として扱い、線形回帰の枠組みを拡張することで、より複雑なデータの関係性を捉えることができます。例えば、2次や3次の多項式を使用することで、曲線的な関係を表現することが可能です。Pythonでは、scikit-learnライブラリを用いて簡単に多項式回帰を実装できます。特に、PolynomialFeaturesクラスを使用して入力データを変換し、線形回帰モデルに適用することで、非線形性を考慮した予測が可能になります。

多項式回帰の利点は、そのシンプルさと解釈の容易さにあります。モデルのパラメータは線形回帰と同様に解釈可能であり、どの程度の非線形性がデータに存在するかを直感的に理解できます。しかし、多項式の次数が高くなると、過学習のリスクが増加する点に注意が必要です。過学習を防ぐためには、適切な次数の選択や正則化手法の適用が重要です。また、多項式回帰は計算コストが比較的低いため、小規模なデータセットやリアルタイム処理にも適しています。

一方で、多項式回帰は非常に複雑な非線形関係を捉えるには限界があります。特に、データの次元が高くなったり、非線形性が極めて複雑な場合には、他の手法との組み合わせや代替手法の検討が必要です。このような場合、ニューラルネットワークのようなより高度な手法が有効となることがあります。多項式回帰は、非線形モデリングの第一歩として理解し、その特性を活かして適切に活用することが重要です。

ニューラルネットワークの基礎

ニューラルネットワークは、人間の脳の神経細胞（ニューロン）を模倣した計算モデルです。このモデルは、入力データを受け取り、複数の層を通過させながら、最終的に出力を生成します。各層はニューロンと呼ばれるユニットで構成され、これらのユニットは重みとバイアスを持ち、データの特徴を学習します。ニューラルネットワークの学習プロセスでは、誤差逆伝播法（バックプロパゲーション）が用いられ、モデルのパラメータを調整することで、予測精度を向上させます。

ニューラルネットワークの重要な特徴の一つは、非線形性を扱えることです。各ニューロンは活性化関数（例：ReLU、シグモイド関数）を通じて非線形変換を行い、複雑なデータのパターンを捉えることができます。これにより、線形モデルでは表現できない複雑な関係性をモデル化することが可能です。特に、深層学習（ディープラーニング）では、多層のニューラルネットワークを使用して、画像認識や自然言語処理などの高度なタスクを実現しています。

ニューラルネットワークの設計においては、層の数やニューロンの数、学習率などのハイパーパラメータを適切に設定することが重要です。これらの設定はモデルの性能に直接影響を与えるため、実験や検証を繰り返しながら最適な値を探る必要があります。また、過学習を防ぐために、ドロップアウトや正則化などの手法も活用されます。ニューラルネットワークは、その柔軟性と高い表現力から、現代の機械学習において中心的な役割を果たしています。

Pythonでの実装：多項式回帰

Pythonでの実装において、多項式回帰は非線形関数モデリングの基本的な手法の一つです。多項式回帰は、線形回帰を拡張したもので、データの非線形な関係を捉えるために使用されます。具体的には、入力変数の多項式項を追加することで、より複雑な曲線をモデル化することが可能です。例えば、2次や3次の多項式を使用することで、データの曲がり具合をより正確に表現できます。

scikit-learnライブラリを使用すると、多項式回帰を簡単に実装できます。まず、PolynomialFeaturesクラスを使用して、入力データの多項式特徴量を生成します。次に、LinearRegressionクラスを使用して、生成された特徴量に対して線形回帰を適用します。これにより、非線形なデータ関係をモデル化することができます。例えば、2次の多項式回帰を適用する場合、入力データの平方項や交差項が自動的に生成され、モデルの精度が向上します。

多項式回帰の利点は、そのシンプルさと計算コストの低さにあります。しかし、高次の多項式を使用すると、過学習のリスクが高まるため、適切な次数を選択することが重要です。また、多項式回帰は、データの局所的な特徴を捉えるのに適していますが、非常に複雑な非線形関係をモデル化するには限界があります。そのため、より高度な手法としてニューラルネットワークが活用されることもあります。

Pythonでの実装：ニューラルネットワーク

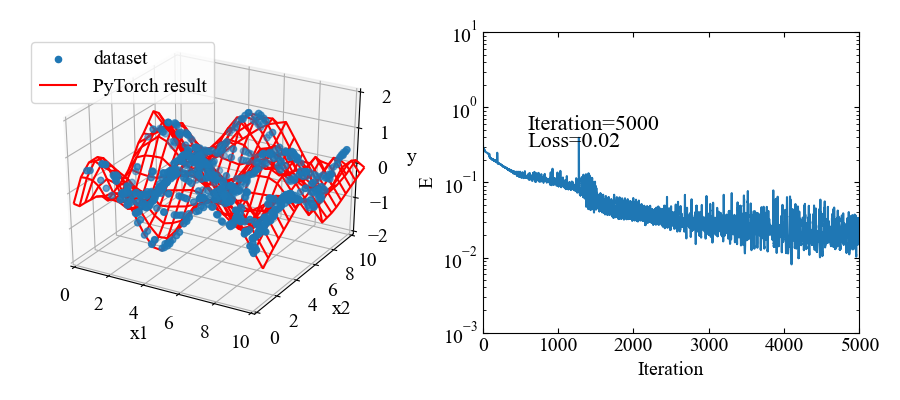
Pythonでの実装において、ニューラルネットワークは非常に強力なツールです。ニューラルネットワークは、人間の脳の神経回路を模倣したアルゴリズムで、複雑な非線形関係をモデル化するのに適しています。Pythonでは、TensorFlowやPyTorchといったライブラリを使用してニューラルネットワークを簡単に構築できます。これらのライブラリは、高度な計算を抽象化し、ユーザーがモデルの設計に集中できるようにします。

ニューラルネットワークの実装では、まず入力層、隠れ層、出力層を定義します。隠れ層の数や各層のニューロン数は、問題の複雑さに応じて調整されます。次に、活性化関数を選択します。活性化関数は、非線形性を導入するために重要で、ReLUやシグモイド関数がよく使われます。最後に、損失関数と最適化アルゴリズムを設定し、モデルを訓練します。

ニューラルネットワークの利点は、非常に高い予測精度を達成できることです。しかし、その反面、計算コストが高く、モデルの解釈が困難であるというデメリットもあります。特に、深層学習モデルでは、なぜ特定の予測が行われたのかを理解するのが難しい場合があります。それでも、ニューラルネットワークは、画像認識や自然言語処理など、多くの分野で成功を収めています。

多項式回帰とニューラルネットワークの比較

多項式回帰とニューラルネットワークは、非線形関数モデリングにおいて広く使用される手法です。多項式回帰は、データに対して多項式関数を適用することで、非線形な関係をモデル化します。この手法は比較的シンプルで計算コストが低いため、小規模なデータセットや単純な非線形関係を扱う場合に適しています。しかし、高次の多項式を使用すると過学習が発生しやすく、モデルの汎化性能が低下するリスクがあります。

一方、ニューラルネットワークは、複数の層とノードを組み合わせて非線形関係を表現する高度な手法です。深層学習の一部としても知られ、非常に複雑なパターンを捉えることが可能です。特に、大規模なデータセットや高次元のデータに対して高い精度を発揮します。ただし、ニューラルネットワークは計算コストが高く、モデルのトレーニングに時間がかかる場合があります。また、モデルの解釈が難しいという課題もあります。

両手法の選択は、データの特性や目的によって異なります。多項式回帰はシンプルで高速なモデリングが必要な場合に適しており、ニューラルネットワークは高度な精度と複雑なパターンの抽出が求められる場面で威力を発揮します。それぞれの長所と短所を理解し、適切な手法を選択することが重要です。

非線形関数モデリングのメリットとデメリット

非線形関数モデリングは、データ間の複雑な関係を捉えるために非常に有用な手法です。高精度な予測が可能であり、特にデータが非線形の関係性を持つ場合にその真価を発揮します。例えば、株価の予測や気象データの分析など、現実世界の多くの問題は線形モデルでは十分に説明できないため、非線形モデリングが重要な役割を果たします。また、非線形関数モデリングを使用することで、データの背後にある隠れたパターンや構造を明らかにすることができます。これにより、より深いデータの理解が可能となり、意思決定の質を向上させることができます。

しかし、非線形関数モデリングにはいくつかのデメリットも存在します。まず、計算コストが高いことが挙げられます。特に、ニューラルネットワークのような複雑なモデルを使用する場合、大量の計算リソースと時間が必要となります。また、非線形モデルはしばしば解釈困難であるという問題もあります。線形モデルと異なり、非線形モデルの結果を直感的に理解するのは難しく、特にビジネス上の意思決定においてはこの点が課題となることがあります。さらに、過学習のリスクも高く、適切な正則化や検証手法を用いることが重要です。

これらのメリットとデメリットを理解し、適切に活用することで、非線形関数モデリングはデータ分析や予測モデルの構築において非常に強力なツールとなります。今後のデータ分析分野では、非線形関数モデリングの重要性がさらに高まることが予想されます。

今後の展望

非線形関数モデリングは、データ分析や機械学習の分野においてますます重要な役割を果たすことが期待されています。特に、多項式回帰やニューラルネットワークといった手法は、複雑なデータパターンを捉えるための強力なツールとして進化を続けています。今後、これらの手法はさらに洗練され、計算コストの削減やモデルの解釈可能性の向上が進むと考えられます。

また、深層学習や自動機械学習（AutoML）の進展により、非線形関数モデリングの適用範囲はさらに広がるでしょう。特に、医療や金融、製造業などの分野では、非線形モデルを活用した高度な予測や分析がますます重要視されることが予想されます。さらに、量子コンピューティングの進化が非線形関数モデリングに新たな可能性をもたらすことも期待されています。

今後の課題としては、モデルの解釈可能性や計算リソースの最適化が挙げられます。特に、ニューラルネットワークのような複雑なモデルでは、その内部構造を理解しやすくすることが重要です。これにより、より信頼性の高い意思決定が可能となり、非線形関数モデリングの応用範囲がさらに広がることが期待されます。

まとめ

非線形関数モデリングは、データ間の複雑な関係を捉えるための強力な手法です。多項式回帰は、線形回帰を拡張し、データの非線形性をモデル化するためのシンプルで効果的な方法です。これにより、データの曲線的な関係を表現することが可能になります。一方、ニューラルネットワークは、より高度な非線形関係をモデル化するための手法であり、特に深層学習の分野で広く活用されています。ニューラルネットワークは、多層構造を持つことで、非常に複雑なパターンや関係を学習することができます。

Pythonでは、scikit-learnやTensorFlow、PyTorchなどのライブラリを使用して、これらの手法を簡単に実装することができます。scikit-learnは多項式回帰の実装に適しており、TensorFlowやPyTorchはニューラルネットワークの構築とトレーニングに最適です。これらのツールを活用することで、非線形関数モデリングのプロセスを効率的に進めることができます。

非線形関数モデリングのメリットは、高精度な予測やデータの深い理解が可能になる点です。しかし、計算コストが高くなることや、モデルの解釈が難しくなるというデメリットも存在します。特にニューラルネットワークの場合、モデルの複雑さが増すほど、その内部の動作を理解することが難しくなります。

将来的には、非線形関数モデリングがデータ分析や機械学習の分野でさらに重要性を増すと予想されます。特に、ビッグデータや複雑なシステムの分析において、非線形モデルの需要は高まっています。これにより、より高度な予測や意思決定が可能になるでしょう。

よくある質問

1. 多項式回帰とニューラルネットワークの違いは何ですか？

多項式回帰は、非線形関係をモデル化するために多項式関数を使用する古典的な統計手法です。これは、入力変数のべき乗を特徴量として追加することで、データの曲線的な関係を捉えます。一方、ニューラルネットワークは、複雑な非線形関係を学習するための高度な機械学習モデルです。ニューラルネットワークは、複数の層とノードを使用して、データのパターンを自動的に抽出し、より柔軟なモデリングが可能です。多項式回帰は解釈が容易ですが、ニューラルネットワークはより高い予測精度を提供する場合があります。

2. Pythonで多項式回帰を実装する際の注意点は何ですか？

Pythonで多項式回帰を実装する際には、過学習に注意する必要があります。多項式の次数が高すぎると、モデルが訓練データに過剰に適合し、未知のデータに対する予測性能が低下する可能性があります。これを防ぐために、交差検証や正則化（例：L2正則化）を活用することが推奨されます。また、特徴量のスケーリングも重要で、特に高次の項を追加する際には、データの標準化や正規化を行うことで計算の安定性を向上させることができます。

3. ニューラルネットワークを用いた非線形関数モデリングの利点は何ですか？

ニューラルネットワークを用いた非線形関数モデリングの主な利点は、高い表現力と柔軟性です。ニューラルネットワークは、複雑なデータ構造や非線形関係を自動的に学習できるため、多項式回帰では捉えきれないパターンをモデル化することが可能です。また、深層学習の技術を活用することで、大規模なデータセットや高次元のデータに対しても効果的に適用できます。ただし、モデルの解釈が難しいことや、計算コストが高いことが課題として挙げられます。

4. 非線形関数モデリングにおいて、どのようにモデルの性能を評価すべきですか？

非線形関数モデリングの性能を評価するためには、訓練データとテストデータを分離し、モデルの汎化性能を確認することが重要です。具体的には、平均二乗誤差（MSE）や決定係数（R²）などの指標を使用して、モデルの予測精度を定量化します。さらに、交差検証を実施することで、モデルの安定性を評価することができます。特にニューラルネットワークの場合、過学習を防ぐために早期停止やドロップアウトなどのテクニックを活用することも有効です。